[Materi kelas7]HIMPUNAN[Relasi Himpunan Irisan dan Gabungan]


Pada topik sebelumnya, kalian telah mempelajari tentang diagram Venn. Diagram Venn adalah salah satu cara menggambarkan suatu himpunan dalam bentuk diagram. Langkah-langkah untuk membuat diagram Venn adalah sebagai berikut.
a. Himpunan semesta S digambarkan dengan persegipanjang.
b. Himpunan lainnya, misalnya A digambarkan menggunakan lingkaran yang terletak di dalam persegipanjang tersebut.
c. Anggota himpunan A digambarkan menggunakan noktah yang terletak di dalam lingkaran.
d. Anggota himpunan S yang bukan anggota A diletakkan di luar lingkaran, tetapi masih di dalam persegipanjang.
Contoh diagram Venn:
 
Pada topik kali ini, kalian akan mempelajari tentang irisan dan gabungan himpunan.
1. Irisan
Definisi
Irisan himpunan A dan B adalah himpunan semua objek yang sekaligus menjadi anggota himpunan A dan anggota himpunan B.
Secara matematis, dapat ditulis: A ∩ B = {x|x ϵ A dan x ϵ B}
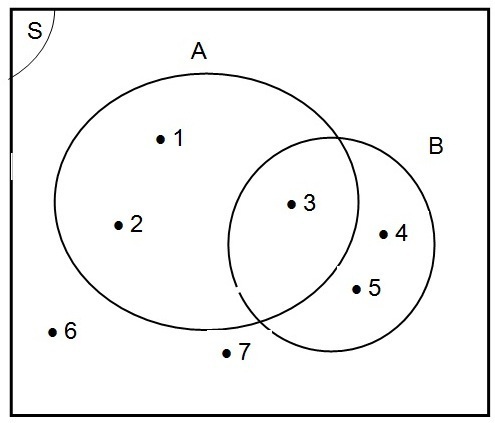
Salah satu diagram Venn yang menunjukkan operasi irisan adalah sebagai berikut.
 
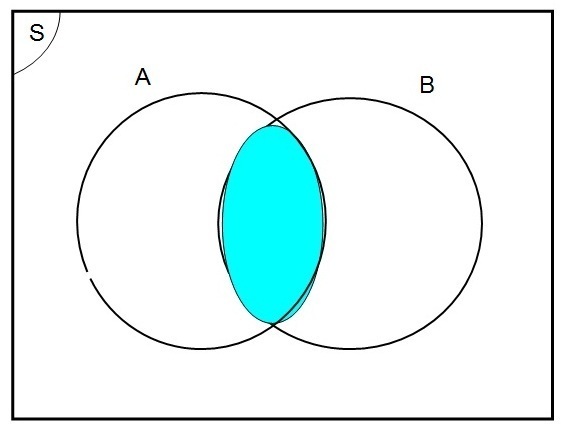
Pada diagram Venn itu, daerah yang berwarna biru menunjukkan daerah himpunan A ∩ B.
Dari pengertian operasi irisan tersebut diperoleh relasi-relasi berikut.
a. Relasi Berpotongan (Joint Sets)
Definisi
Dua buah himpunan disebut saling berpotongan jika dan hanya jika irisannya bukan himpunan kosong. Secara matematis dapat ditulis sebagai berikut.
 
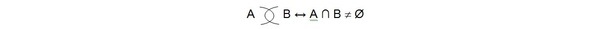
Contoh:
Dari himpunan A = {1, 2, 4} dan B = {0, 2, 3, 4}, diperoleh A ∩ B = {2, 4}.
Berarti, A ∩ B ≠ Ø sehingga himpunan A dan B saling berpotongan.
b. Relasi Saling Lepas (Disjoint Sets)
Definisi
Dua buah himpunan disebut saling lepas jika dan hanya jika irisannya merupakan himpunan kosong.
Secara matematis, dapat ditulis: A )( B ↔ A ∩ B = Ø
Contoh:
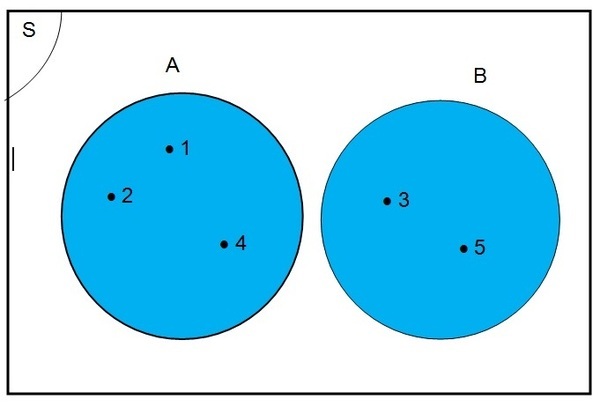
Dari himpunan A = {1, 2, 4} dan B = {3, 5}, diperoleh A ∩ B = Ø sehingga himpunan A dan B saling lepas.
Diagram Venn-nya sebagai berikut.

2. Gabu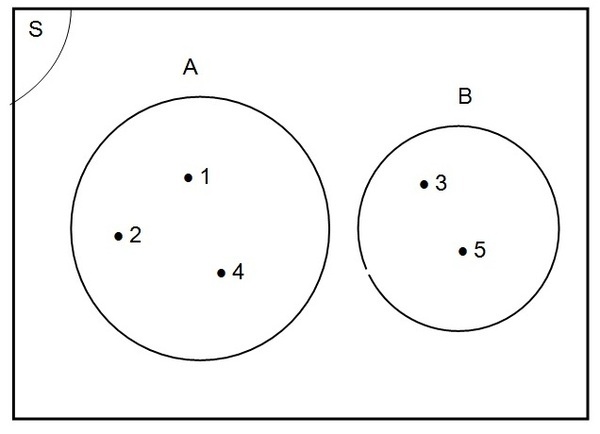ngan
Definisi
Gabungan himpunan A dan B adalah himpunan yang meliputi semua anggota himpunan A dan B.
Secara matematis dapat ditulis: A U B = {x|x ϵ A atau x ϵ B}
Kata “atau” dalam pengertian di atas bersifat inklusif, yaitu untuk x anggota A saja, x anggota B saja, dan x anggota irisannya.
Contoh:
Diketahui S adalah himpunan bilangan asli yang kurang dari 6, A = {1, 2, 4}, dan B = {3, 5}. Coba tentukan A U B dan gambarkan diagram Venn-nya.
Jawab:
Oleh karena S adalah himpunan bilangan asli yang kurang dari 6, A = {1, 2, 4}, dan B = {3, 5}, maka A U B = {1, 2, 3, 4, 5} = S.
Diagram Venn-nya sebagai berikut.
 

Komentar

Posting Komentar

Postingan populer dari blog ini

[Materi Kelas 8]LINGKARAN[Segiempat Tali Busur]

Gambar
❀✿❁ Segiempat Tali Busur ❁✿❀ Sebelum kita mempelajari topik ini, mari simak percakapatan di antara dua sahabat berikut. Anton : Budi, kamu pernah melihat tanda  STOP  di jalan kan? Budi : Pernah Ton, yang warnanya merah dan putih itu kan? Anton : Iya, itu terdiri dari lingkaran berwarna merah dan segiempat yang berwarna putih ya? Segiempatnya itu berada di tengah lingkaran. Budi : Itu namanya segiempat talibusur Ton. Anton : Apa itu segiempat tali busur Bud? Budi : Aku juga belum begitu tahu, mari kita tanya ke bu guru untuk lebih jelasnya. Kemudian, Anton dan Budi menemui ibu guru. Ayo simak jawaban bu guru agar kita dapat memahami tentang segiempat tali busur bersama Anton dan Budi. Segiempat Tali Busur Perhatikan gambar lingkaran di bawah ini. Pada lingkaran, A adalah titik pusat lingkaran, sedangkan titik B, C, D dan E terletak pada lingkaran. CD, BC, EB, DE adalah tali busur dari lingkaran. Tali busur tersebut membentuk sebuah bangun segiempat yang disebut  Seg
Lihat Selanjutnya >>

Seputar Asal Mula Resep Pintar Sofi

Semangat pagi pengunjung ^^ Sekilas info aja tentang awal pembuatan resep ini yaa. resep ini didirikan pada tahun 2015, tepatnya saat Lembaga Bimbingan Belajar YO diresmikan. LBB YO? iya, LBB YO adalah Bimbingan Belajar Privat yang didirikan oleh Ir. Yudi Susanto a.k.a CEO LBB YO. Alhamdulillah, sampai sekarang Blog ini masih hidup, dan Bimbingan Belajar kami semakin berkembang. Bagi yang berminat untuk mengasah kemampuan, terus ikuti perkembangan kami^^  Untuk info lebih lanjut hubungi : 085850687400 (Sophia Sal Sabila a.k.a Manager LBB YO)
Lihat Selanjutnya >>

[Materi Kelas 8]LINGKARAN[Garis Singgung Persekutuan]

Gambar
GARIS SINGGUNG PERSEKUTUAN Pernahkah kalian melihat rantai yang bergerak pada sepeda motor ataupun sepeda? Rantai pada sepeda motor atau sepeda berfungsi untuk menghubungkan poros roda depan dan poros roda belakang, sehingga kedua roda dapat berputar. Dalam kasus ini, rantai dikatakan menyinggung kedua poros roda yang berupa lingkaran dan disebut sebagai garis singgung persekutuan dua lingkaran. Dalam topik ini, kalian akan belajar mengenai garis singgung persekutuan dua lingkaran, yang terdiri atas dua macam, yaitu garis singgung persekutuan luar garis singgung persektuan dalam Apa perbedaan dari kedua garis singgung persekutuan tersebut? Yuk temukan jawabannya dalam topik kali ini. GARIS SINGGUNG PERSEKUTUAN LUAR Pada gambar di bawah ini, garis SR dan garis PQ sama-sama menyinggung lingkaran A maupun lingkaran B. Adapun kedua garis tersebut tidak berpotongan di antara kedua lingkaran. Nah, kedua garis tersebut disebut garis singgung persekutuan luar.
Lihat Selanjutnya >>