[Materi Kelas 8]LINGKARAN[Garis Singgung Lingkaran]


Pernahkah kalian menimba air di sumur atau melihat katrol pada sumur timba?
Jika kalian perhatikan ilustrasi di atas, ada sebuah tali yang melilit katrol. Tali tersebut berfungsi untuk menarik ember dari dalam sumur. Nah, pada saat tali ditarik, katrol tersebut akan berputar. Dalam kasus seperti ini, tali yang digunakan untuk menarik ember dikatakanmenyinggung katrol yang berbentuk lingkaran.
Apa yang dimaksud dengan menyinggung lingkaran?
Yuk temukan jawabannya dalam topik kali ini.

GARIS SINGGUNG LINGKARAN
Pada topik kali ini, kalian akan belajar tentang garis singgung lingkaran dan sifat-sifatnya.
Nah, sebelumnya mari kita perhatikan dahulu gambar lingkaran berikut ini.
Lingkaran di atas berpusat di titik O, dimana garis k memotong lingkaran di titik A, garis lmemotong lingkaran di titik B dan C, sedangkan garis m memotong lingkaran di titik D.
Nah, sebuah garis dikatakan menyinggung lingkaran, jika garis tersebut memotong lingkaran tepat pada satu titik.
Pada gambar di atas, manakah yang merupakan garis singgung lingkaran?
Ya, tentu saja garis k dan garis m.

SIFAT GARIS SINGGUNG LINGKARAN
Bagaimanakah sifat garis singgung lingkaran?
Yuk kita cermati lingkaran berikut ini sebelum menjawab pertanyaan di atas.
Pada lingkaran di atas, tampak bahwa garis l tegak lurus dengan diameter lingkaran, yaitu AD.
Oleh karena garis k dan garis m sejajar dengan garis l, maka garis k dan garis m juga tegak lurus dengan diameter AD.
Selanjutnya, karena garis k tegak lurus dengan diameter AD, maka garis k juga tegak lurus dengan jari-jari OA. Dengan demikian, garis m tegak lurus dengan jari-jari OD, sebab garis mtegak lurus dengan diameter AD.
Jadi, dapat kita simpulkan bahwa garis singgung lingkaran akan tegak lurus dengan jari-jari lingkaran yang melewati titik singgung.

PANJANG GARIS SINGGUNG LINGKARAN
Nah, bagaimana dengan panjang garis singgung lingkaran? Bagaimana cara menentukannya?
Yuk kita perhatikan gambar berikut.
Pada gambar di atas, dari titik C ditarik dua buah garis sehingga masing-masing garis tersebut menyinggung lingkaran. Kedua garis tersebut adalah garis k dan garis m. Titik singgung antara lingkaran dan garis k adalah titik A, sedangkan titik singgung antara lingkaran dan garism adalah titik B.
Berdasarkan sifat garis singgung, maka garis k tegak lurus dengan jari-jari OA, sedangkan garis m tegak lurus dengan jari-jari OB. Dengan demikian, segitiga OAC tegak lurus di titik Adan segitiga OBC tegak lurus di titik B.
Tentunya kalian masih ingat dengan teorema Pythagoras yang telah kalian pelajari pada topik sebelumnya bukan?
Berdasarkan teorema Pythagoras,

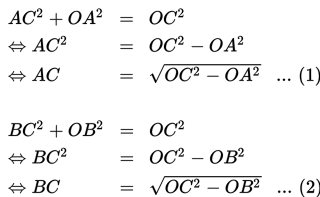
Oleh karena OA dan OB merupakan jari-jari lingkaran, maka OA dan OB mempunyai panjang yang sama. Dengan demikian, ruas kanan dari persamaan (1) dan persamaan (2) pada uraian di atas memberikan hasil yang sama. Dengan kata lain, garis singgung AC dan garis singgungBC mempunyai panjang yang sama.
Jadi, dapat kita simpulkan bahwa
  1. Melalui sebuah titik di luar lingkaran, dapat dibuat dua buah garis singgung lingkaran.
  2. Dua buah garis singgung lingkaran yang ditarik dari sebuah titik di luar lingkaran mempunyai panjang yang sama.

CONTOH
Apakah kalian sudah paham dengan materi pada topik kali ini?
Agar kalian semakin paham, yuk kita cermati beberapa contoh berikut.

Contoh 1:
Perhatikan gambar berikut.
Pada lingkaran di atas, garis AC merupakan garis singgung lingkaran yang ditarik dari titik C. Jika panjang garis AC adalah 24 cm dan panjang jari-jari lingkaran adalah 7 cm, maka berapakah panjang garis PC?
Penyelesaian:
Oleh karena garis AC merupakan garis singgung lingkaran, maka segitiga PAC tegak lurus di titik A.
Berdasarkan teorema Pythagoras,
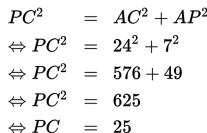
Jadi, panjang garis PC adalah 25 cm.

Contoh 2:
Tentukan panjang garis DC pada gambar berikut.
Penyelesaian:
Oleh karena garis AC dan DC merupakan garis singgung lingkaran besar yang ditarik dari titik C, maka garis AC dan DC mempunyai panjang yang sama → AC = DC.
Oleh karena garis DC dan BC merupakan garis singgung lingkaran kecil yang ditarik dari titik C, maka garis DC dan BC mempunyai panjang yang sama → DC = BC.
Dengan demikian, garis AC dan garis BC mempunyai panjang yang sama → AC = BC = DC.

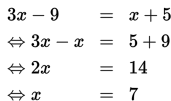
Oleh karena AC = BC = DC, maka panjang garis DC adalah x + 5 = 7 + 5 = 12 cm.

Komentar

Posting Komentar

Postingan populer dari blog ini

[Materi Kelas 8]LINGKARAN[Segiempat Tali Busur]

Gambar
❀✿❁ Segiempat Tali Busur ❁✿❀ Sebelum kita mempelajari topik ini, mari simak percakapatan di antara dua sahabat berikut. Anton : Budi, kamu pernah melihat tanda  STOP  di jalan kan? Budi : Pernah Ton, yang warnanya merah dan putih itu kan? Anton : Iya, itu terdiri dari lingkaran berwarna merah dan segiempat yang berwarna putih ya? Segiempatnya itu berada di tengah lingkaran. Budi : Itu namanya segiempat talibusur Ton. Anton : Apa itu segiempat tali busur Bud? Budi : Aku juga belum begitu tahu, mari kita tanya ke bu guru untuk lebih jelasnya. Kemudian, Anton dan Budi menemui ibu guru. Ayo simak jawaban bu guru agar kita dapat memahami tentang segiempat tali busur bersama Anton dan Budi. Segiempat Tali Busur Perhatikan gambar lingkaran di bawah ini. Pada lingkaran, A adalah titik pusat lingkaran, sedangkan titik B, C, D dan E terletak pada lingkaran. CD, BC, EB, DE adalah tali busur dari lingkaran. Tali busur tersebut membentuk sebuah bangun segiempat yang disebut  Seg
Lihat Selanjutnya >>

Seputar Asal Mula Resep Pintar Sofi

Semangat pagi pengunjung ^^ Sekilas info aja tentang awal pembuatan resep ini yaa. resep ini didirikan pada tahun 2015, tepatnya saat Lembaga Bimbingan Belajar YO diresmikan. LBB YO? iya, LBB YO adalah Bimbingan Belajar Privat yang didirikan oleh Ir. Yudi Susanto a.k.a CEO LBB YO. Alhamdulillah, sampai sekarang Blog ini masih hidup, dan Bimbingan Belajar kami semakin berkembang. Bagi yang berminat untuk mengasah kemampuan, terus ikuti perkembangan kami^^  Untuk info lebih lanjut hubungi : 085850687400 (Sophia Sal Sabila a.k.a Manager LBB YO)
Lihat Selanjutnya >>

[Materi Kelas 8]LINGKARAN[Garis Singgung Persekutuan]

Gambar
GARIS SINGGUNG PERSEKUTUAN Pernahkah kalian melihat rantai yang bergerak pada sepeda motor ataupun sepeda? Rantai pada sepeda motor atau sepeda berfungsi untuk menghubungkan poros roda depan dan poros roda belakang, sehingga kedua roda dapat berputar. Dalam kasus ini, rantai dikatakan menyinggung kedua poros roda yang berupa lingkaran dan disebut sebagai garis singgung persekutuan dua lingkaran. Dalam topik ini, kalian akan belajar mengenai garis singgung persekutuan dua lingkaran, yang terdiri atas dua macam, yaitu garis singgung persekutuan luar garis singgung persektuan dalam Apa perbedaan dari kedua garis singgung persekutuan tersebut? Yuk temukan jawabannya dalam topik kali ini. GARIS SINGGUNG PERSEKUTUAN LUAR Pada gambar di bawah ini, garis SR dan garis PQ sama-sama menyinggung lingkaran A maupun lingkaran B. Adapun kedua garis tersebut tidak berpotongan di antara kedua lingkaran. Nah, kedua garis tersebut disebut garis singgung persekutuan luar.
Lihat Selanjutnya >>