[Materi Kelas 8]LINGKARAN[Garis Singgung Persekutuan]

GARIS SINGGUNG PERSEKUTUAN

Pernahkah kalian melihat rantai yang bergerak pada sepeda motor ataupun sepeda?

Rantai pada sepeda motor atau sepeda berfungsi untuk menghubungkan poros roda depan dan poros roda belakang, sehingga kedua roda dapat berputar. Dalam kasus ini, rantai dikatakan menyinggung kedua poros roda yang berupa lingkaran dan disebut sebagai garis singgung persekutuan dua lingkaran.

Dalam topik ini, kalian akan belajar mengenai garis singgung persekutuan dua lingkaran, yang terdiri atas dua macam, yaitu

• garis singgung persekutuan luar
• garis singgung persektuan dalam

Apa perbedaan dari kedua garis singgung persekutuan tersebut?
Yuk temukan jawabannya dalam topik kali ini.

GARIS SINGGUNG PERSEKUTUAN LUAR

Pada gambar di bawah ini, garis SR dan garis PQ sama-sama menyinggung lingkaran A maupun lingkaran B. Adapun kedua garis tersebut tidak berpotongan di antara kedua lingkaran. Nah, kedua garis tersebut disebut garis singgung persekutuan luar.

Bagaimana cara menentukan panjang garis singgung persekutuan luar?
Yuk kita cermati penjelasan berikut.

Pada gambar di atas, panjang jari-jari lingkaran A adalah R, panjang jari-jari lingkaran B adalahr, jarak antara kedua pusat lingkaran sama dengan panjang garis AB, dan garis SR adalah garis singgung persekutuan luar.

Jika garis ST sejajar dengan garis RB, maka kedua garis tersebut mempunyai panjang yang sama dan panjang garis TB sama dengan panjang garis SR → ST = RB = r dan TB = SR.

Dengan demikian, BRST merupakan sebuah bangun persegi panjang dimana besar sudut T adalah 90°. Dengan kata lain, segitiga TAB siku-siku di titik T.

Berdasarkan teorema Pythagoras,

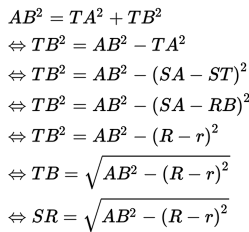
Berdasarkan uraian di atas, dapat kita simpulkan bahwa untuk menentukan panjang garis singgung persekutuan luar (SR), kita perlu mengetahui jarak antara kedua pusat lingkaran (AB)dan panjang jari-jari kedua lingkaran (R dan r).

GARIS SINGGUNG PERSEKUTUAN DALAM

Pada gambar di atas, garis SQ dan garis PR sama-sama menyinggung lingkaran A maupun lingkaran B. Adapun kedua garis tersebut berpotongan di antara kedua lingkaran. Nah, kedua garis tersebut disebut garis singgung persekutuan dalam.

Bagaimana cara menentukan panjang garis singgung persekutuan dalam?
Yuk kita cermati penjelasan berikut.

Pada gambar di atas, panjang jari-jari lingkaran A adalah R, panjang jari-jari lingkaran B adalahr, jarak antara kedua pusat lingkaran sama dengan panjang garis AB, dan garis SQ adalah garis singgung persekutuan dalam.

Jika garis TS sejajar dengan garis BQ, maka kedua garis tersebut mempunyai panjang yang sama dan panjang garis TB sama dengan panjang garis SQ → TS = BQ = r dan TB = SQ.

Dengan demikian, TBQS merupakan sebuah bangun persegi panjang dimana besar sudut T adalah 90°. Dengan kata lain, segitiga TAB siku-siku di titik T.

Berdasarkan teorema Pythagoras,

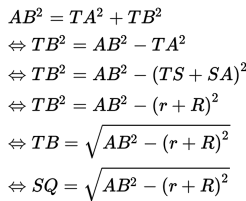
Berdasarkan uraian di atas, dapat kita simpulkan bahwa untuk menentukan panjang garis singgung persekutuan dalam (SQ), kita perlu mengetahui jarak antara kedua pusat lingkaran(AB) dan panjang jari-jari kedua lingkaran (R dan r).

CONTOH

Tentunya kalian sudah paham mengenai bagaimana cara menentukan panjang garis singgung persekutuan luar dan garis singgung persekutuan dalam bukan?
Yuk kita cermati beberapa contoh berikut untuk menambah pemahaman kalian.

Contoh 1:

Diberikan dua buah lingkaran dengan panjang jari-jari 3 cm dan 2 cm. Jika jarak kedua pusat lingkaran adalah 13 cm, maka berapakah panjang garis singgung persekutuan dalam kedua lingkaran tersebut?

Penyelesaian:

Permasalahan dalam soal dapat kita ilustrasikan sebagai berikut:

Berdasarkan informasi dalam soal,

• jarak antara kedua pusat lingkaran adalah 13 cm → AB = 13 cm
• panjang jari-jari lingkaran besar adalah 3 cm→ R = 3 cm
• panjang jari-jari lingkaran kecil adalah 2 cm → r = 2 cm.

Dengan demikian,

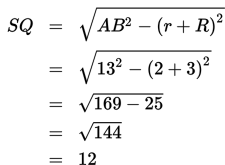
Jadi, panjang garis singgung persekutuan dalam kedua lingkaran adalah 12 cm.

Contoh 2:

Diberikan dua buah lingkaran dengan panjang jari-jari 10 cm dan 2 cm. Jika jarak kedua pusat lingkaran adalah 17 cm, maka berapakah panjang garis singgung persekutuan dalam kedua lingkaran tersebut?

Penyelesaian:

Permasalahan di atas dapat diilustrasikan sebagai berikut:

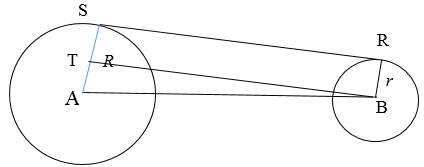
Berdasarkan informasi dalam soal,

• jarak antara kedua pusat lingkaran adalah 17 cm → AB = 17 cm
• panjang jari-jari lingkaran besar adalah 10 cm→ R = 10 cm
• panjang jari-jari lingkaran kecil adalah 2 cm → r = 2 cm.

Dengan demikian,

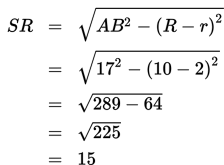
Jadi, panjang garis singgung persekutuan luar kedua lingkaran adalah 15 cm.