[Materi kelas7]HIMPUNAN[Operasi Himpunan]
Pada topik kali ini, kita akan membahas operasi pada
himpunan. Sebelum mempelajari materi tersebut, terlebih dahulu kita akan
membahas tentang himpunan bagian.
1. Himpunan Bagian
Definisi
Himpunan A merupakan himpunan bagian dari B jika dan hanya
jika setiap anggota A juga menjadi anggota B.
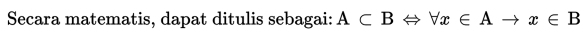
Didefinisikan pula bahwa setiap himpunan kosong merupakan
bagian dari himpunan lainnya.
Contoh:
Himpunan bagian dari B = {1, 2} adalah Ø, {1}, {2}, dan {1, 2}.
Tampak bahwa jika n(B) = 2 maka banyak himpunan bagiannya ada 4 = 22.
Secara umum dapat dirumuskan bahwa:
Contoh:
Himpunan bagian dari B = {1, 2} adalah Ø, {1}, {2}, dan {1, 2}.
Tampak bahwa jika n(B) = 2 maka banyak himpunan bagiannya ada 4 = 22.
Secara umum dapat dirumuskan bahwa:
Sifat
jika A adalah suatu himpunan dengan n(A) = k maka banyaknya
himpunan bagian dari A adalah 2k
Apakah kalian sudah paham?
Sekarang, mari kita lanjutkan pada pembahasan operasi pada himpunan.
Sekarang, mari kita lanjutkan pada pembahasan operasi pada himpunan.
2. Operasi Komplemen
Definisi
Operasi komplemen didefinisikan sebagai berikut.
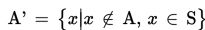
Dibaca “himpunan A’ anggotanya adalah x sedemikian sehingga
x bukan anggota A, tapi x anggota S.”
Contoh:
Diketahui S adalah himpunan bilangan asli yang kurang dari 7 dan A = {2, 3, 5}. Coba tentukan A’ dan gambarkan diagram Venn-nya.
Jawab:
S = {1, 2, 3, 4, 5, 6, 7} dan A = {2, 3, 5}
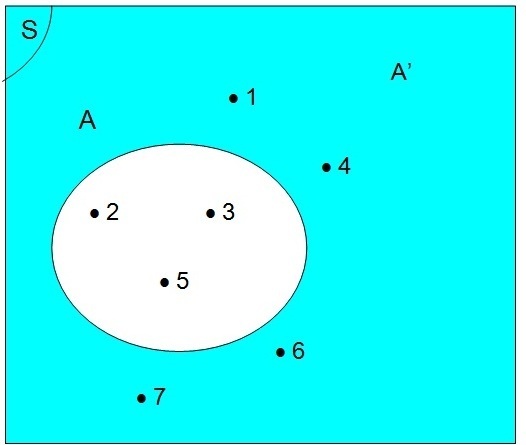
Berdasarkan pengertian operasi komplemen, diperoleh A’ = {1, 4, 6, 7}.
Diagram Venn-nya seperti berikut.
Diketahui S adalah himpunan bilangan asli yang kurang dari 7 dan A = {2, 3, 5}. Coba tentukan A’ dan gambarkan diagram Venn-nya.
Jawab:
S = {1, 2, 3, 4, 5, 6, 7} dan A = {2, 3, 5}
Berdasarkan pengertian operasi komplemen, diperoleh A’ = {1, 4, 6, 7}.
Diagram Venn-nya seperti berikut.
3. Operasi Pengurangan
Definisi
Operasi pengurangan dua buah himpunan dinotasikan dengan
“-“, didefinisikan sebagai berikut.
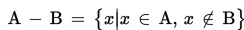
Contoh:
Dari himpunan A = {1, 3, 5, 7} dan B = {2, 4, 6, 8}, diperoleh A – B = {1, 3, 5, 7} = A. Kamu pun dapat mengamati bahwa A dan B adalah himpunan yang saling lepas. Ternyata, untuk himpunan yang saling lepas ini, selisihnya sama dengan himpunan yang dikurangi.
Dari himpunan A = {1, 3, 5, 7} dan B = {2, 4, 6, 8}, diperoleh A – B = {1, 3, 5, 7} = A. Kamu pun dapat mengamati bahwa A dan B adalah himpunan yang saling lepas. Ternyata, untuk himpunan yang saling lepas ini, selisihnya sama dengan himpunan yang dikurangi.
Komentar